Последовательное и параллельное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
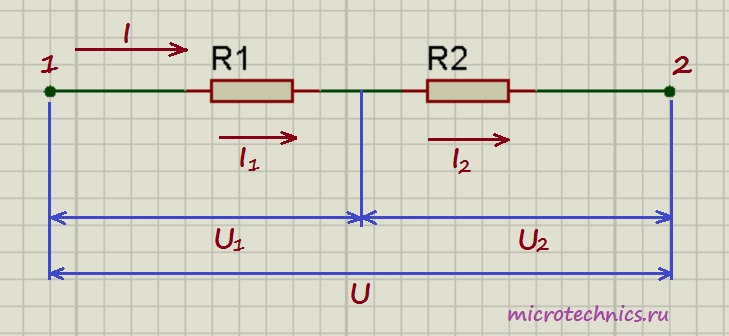
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:


Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

Но для общего напряжение также справедлив закон Ома:

Здесь – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
– это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
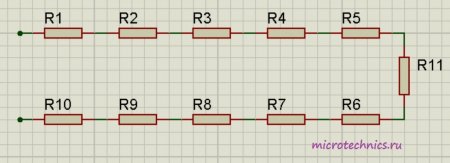
Общее сопротивление будет равно:

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае А если при последовательном соединении все сопротивления равны (
А если при последовательном соединении все сопротивления равны ( ), то общее сопротивление цепи составит:
), то общее сопротивление цепи составит:

 в данной формуле равно количеству элементов цепи.
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
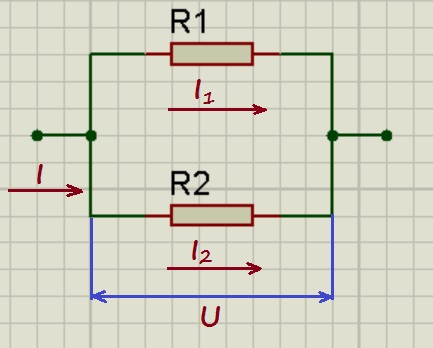
При параллельном соединении напряжения на проводниках равны:

А для токов справедливо следующее выражение:

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:


Подставим эти выражения в формулу общего тока:

А по закону Ома ток:

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

Данную формулу можно записать и несколько иначе:

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
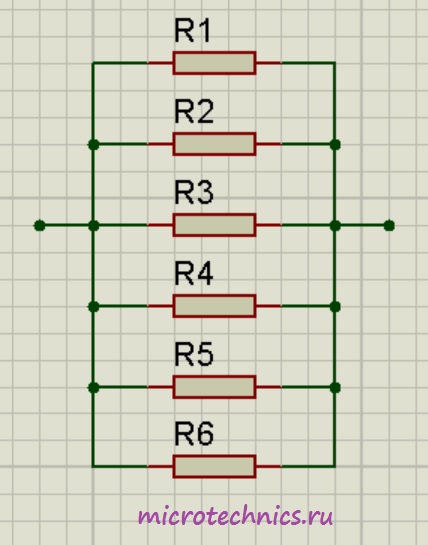

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
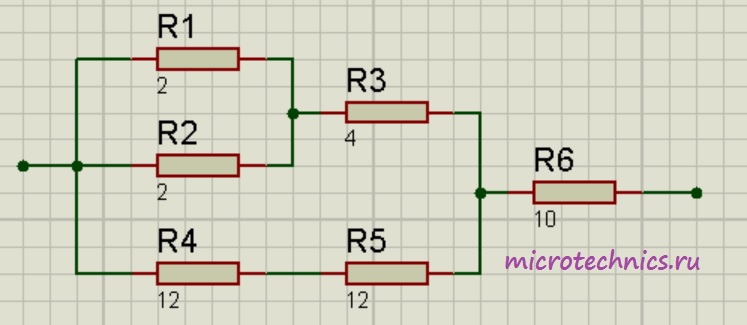
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов и
и  – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором
– они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором  :
:

Теперь у нас образовались две группы последовательно соединенных резисторов:
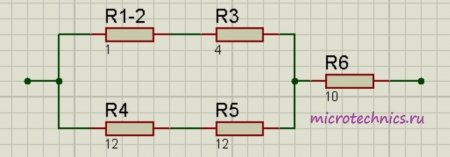
Заменим эти две группы двумя резисторами, сопротивление которых равно:


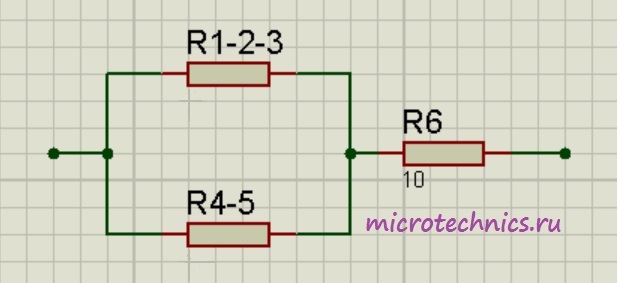
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов и
и  одним резистором
одним резистором  :
:

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
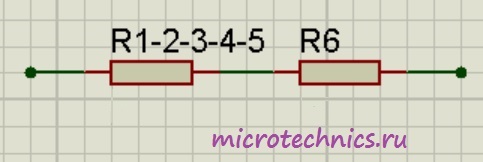
Общее сопротивление цепи получилось равным:

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов.
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях.
Сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:

Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов
Теперь у нас образовались две группы последовательно соединенных резисторов:

и
и
Заменим эти две группы двумя резисторами, сопротивление которых равно:

Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов.
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях.

Нет комментариев. Гость, не желаешь оставить первый комментарий?
Перед публикацией, советую ознакомится с правилами!
Комментарии

Новый адрес сайта
Влад,хорошая идея!ЗА
Новый адрес сайта
Сделайте ув файлах стол заказов.можно будет выкладывать программы и т.п
Теплотехнические измерения и приборы. В.П. Преображенский, 1978
Лучшая книга!

Датчик уровня Радон У
@Oleg да. Теплоприбор
Датчик уровня Радон У
Сейчас актуальны такие датчики?
Все комментарии..
Полный список последних комментариев

